カイ二乗検定の基本はクロス表にあり
前回はt検定を取り上げましたが、今回はカイ二乗検定と相関係数の検定(無相関検定)をとりあげます。カイ二乗検定とは、2つの名義尺度の変数の間に関連があるか、それとも独立であるかを見るものです。カイ二乗検定で分析した論文を読んで、いったいどういうクロス表で計算したのかわからないということがたびたびあります。たとえば、次のように書いてあったらいかがでしょう。どのようなクロス表で計算したかわかるでしょうか。
カイ二乗検定の結果、日本語母語話者は、日本語非母語話者より、1番と2番の項目を選んだ割合が多い。
表1は1番の結果ですが、このように、項目ごとにクロス表を作って、項目数の回数カイ二乗検定を行ったかもしれませんし、表2のように、全体のクロス表を作って、カイ二乗検定を1回行ったのかもしれません。どちらだったかは、結果に自由度が記載されていれば見当がつきますが、書かれていないとまったくわかりません。ちなみに、表1の場合の自由度は1(2×2のクロス表なので、(2-1)×(2-1)となります)、表2の場合の自由度は3(2×4のクロス表なので、(2-1)×(4-1)となります)となります。
表1 1番の結果(人数)
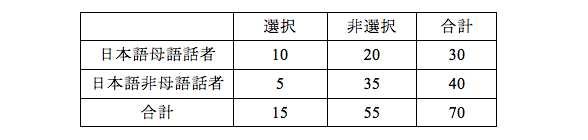
表2 1番から4番の結果(人数)
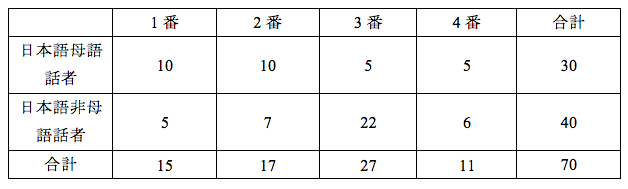
カイ二乗検定のように、2変量の独立性の検定をする場合は、原則的にクロス表を示します。上の表は観測度数(実際に得られた値)を記載しただけですが、これに期待度数を加えるのが一般的です。次の表3の( )内の数字が期待度数です。期待度数というのは、クロス表に偏りがない(独立である)ことを想定した値、すなわち全体の回答結果の傾向を反映した値となります。表3の場合、「1番を選択した人」は日本語母語話者と日本語非母語話者を合わせて、70人中15人(約21.4%)です。もし、日本語母語話者と日本語非母語話者の回答に偏りがなければ、同者とも21.4%ほどの人が選択しているはずです。日本語母語話者30人のうち、21.4%に当たるのは6.4人であり、この数値が「日本語母語話者」で「1番を選択した人」の期待度数となります。このように計算した期待度数を書き込んだのが表3です。表3を見ると、日本語母語話者の「選択」は期待度数(6.4)よりも観測度数(10)の方が多く、反対に、日本語非母語話者は期待度数(8.6)のほうが多いことがわかります。このように書くと、観測度数と期待度数を簡単に比較することができ、カイ二乗の結果も容易に理解できます。期待度数のかわりにパーセントで表す論文を見ることがありますが、そのパーセントが全体の合計の中での割合なのか、行で合計した時の割合なのか、列で合計した時の割合なのか、一見してわかりません。そのような意味でも期待度数を書くのが推奨されます。
表3 1番の結果(人数、期待度数入り)
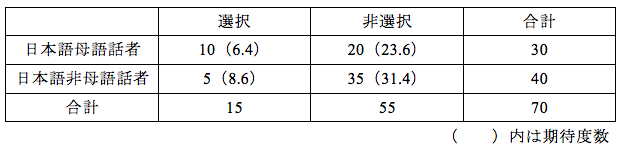
カイ二乗検定はクロス表をまとめて示すことが基本ですが、グラフで割合を示すのみの論文があります。例えば次のグラフは、この連載の初回で示したものです。これでは、観測度数も期待度数も自由度もわかりませんし、どのようなクロス表でカイ二乗検定を行ったのかすぐには理解できません。グラフは一見して、違いがわかるという利点はありますが、カイ二乗検定の結果を報告にするには、観測度数、期待度数、自由度、カイ二乗検定の結果、有意確率を報告することが求められます。グラフで示してはいけないわけではありませんが、まずはクロス表を示すのがいいでしょう。
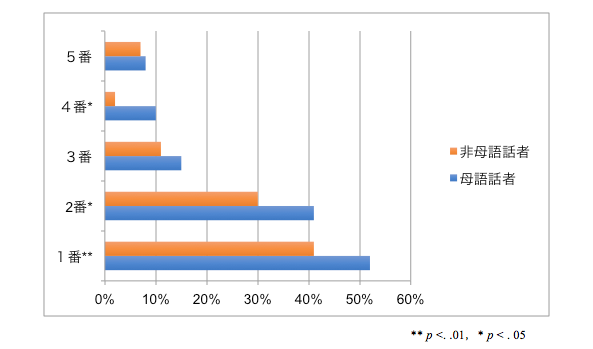
図1 カイ二乗検定の結果をグラフ化した例
カイ二乗検定の結果の報告のしかた
次に、カイ二乗検定の結果を報告する文ですが、次のような記述を見ることがあります。
授業の満足の程度に関して、グループAとBの間に1%水準で有意差が認められた(χ2(3)=8.921, p<.01)。
前回取り上げたt検定は平均値の差の検討なので「有意差」という表現を使用しますが、カイ二乗検定で、「有意差があった」という表現は適切ではありません。では、どのように言うかというと、有意確率が有意水準以下だった場合は、「関連がある」「偏りがある」などの表現を使用します。先の例では、次のようになります。
授業の満足の程度に関して、グループAとBの間に偏りがあった(χ2(3)=8.921, p<.01)。
もし、「偏りがあった」という表現がわかりにくい場合は、次のように書いてもいいと思います。
カイ二乗検定の結果、グループAの方がグループBよりも○○と回答した人が多いことがわかった(χ2(3)=8.921, p<.01)。
相関係数は一致度の計算には向いていない
カイ二乗検定は、名義尺度の2つの変数の間の独立性(関連性がないこと)を見るための検定法でしたが、2つの変数が間隔尺度・比(率)尺度の場合には相関係数が指標として用いられ、2つの変数間に関連がない場合に、「無相関検定」が用いられます。
相関係数も多くの研究で扱われています。例えば、作文や会話などのパフォーマンステストについて、2人の評定者の間の評定の一致度を検討するときに、相関係数を用いる研究があります。しかし、正確に言うと、相関係数では一致度を見ることはできません。表4は、ある作文テストの評価結果を表しています。5人の学生が書いた作文を評定者3人が5段階で評定しています。
表4 ある作文テストの評価結果
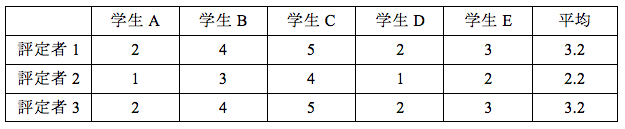
評定者1と評定者3は、全く同じ結果なので、相関係数を計算すると1.0になります。散布図で表すと図2のようになり、両者の評定が完全に一致して直線状に並んでいることがわかります。評定者1と2は、同じ結果ではありませんが、相関係数を計算すると1.0になります。散布図で表すと図3のようになります。評定者2の評価結果に1を加えると評定者1の結果になり、この組み合わせも直線状に並んでいます。これらの例のように、データが直線上にプロットされる場合、相関係数は1.0になります。
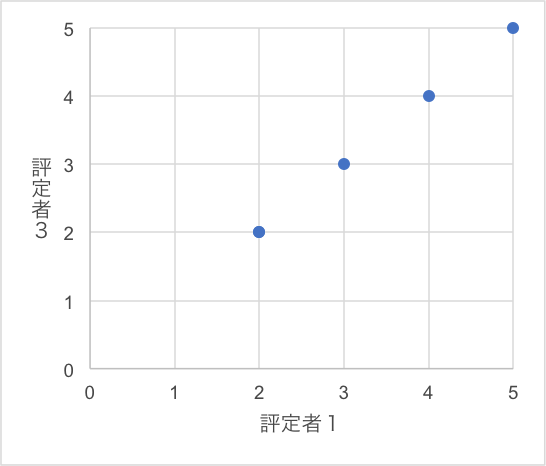
図2 評定者1と評定者3の結果
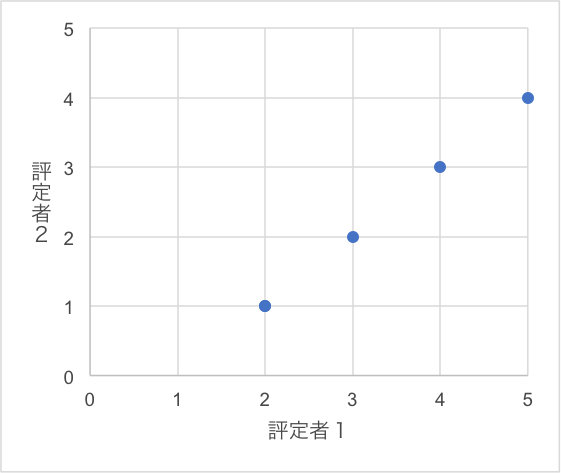
図3 評定者1と評定者2の結果
しかし、図2の結果と図3の結果を同じ一致度と解釈してもいいのでしょうか。表4の平均値を見ると、評定者1は3.2、評定者2は2.2であり、5点満点で考えると大きな違いと言えます。つまり、相関係数は1.0であっても、評定者1と3の組み合わせのようにまったく同じ結果というわけではないのです。このように、相関係数では、2変量間の一致度を正確に見ることはできないのです。特に、平均値が異なる場合は、相関係数ではなく、κ(カッパ)係数(厳密には、重み付きκ系数)を計算するべきです。κ係数であれば、2変量間の一致度がわかります。ちなみに、表4の評定者1と評定者2の間でκ係数を計算すると、0.83になり、相関係数(1.0)とは異なる結果となります。κ係数の計算法に関しては、例えば、野口・大隅(2014)などを参照して下さい。
有意な相関とは?
相関係数の結果を報告する文に次のようなものがあります。「有意な相関」とはどういうことでしょうか。
語彙テストの得点と聴解テストの得点は有意な相関を示している。
相関の検定を理解していない読者は、「相関係数が高い」「強い相関関係になる」と理解してしまいそうです。ここでの「相関の検定」は、先に述べた「無相関検定」で、「2変量の相関係数が母集団でゼロである」という検定仮説を検定するものです。つまり、有意水準(例えば5%)以下であれば、検定仮説が棄却されますので「2変量の相関はゼロではない」ということを示します。ゼロではないだけで、「強い」相関関係にあるとは言えないのです。相関の度合いに言及するのであれば、相関係数の値を参照する必要があります。
表5 相関係数の例
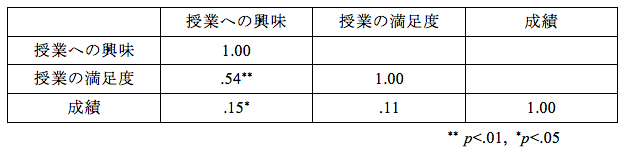
例えば、表5は授業内容に対する評価と成績の相関を示したものです。授業への興味と成績の間の相関係数は0.15で、この値を見る限り、相関はほとんどなさそうです。しかし、無相関検定では「5%水準で有意」という結果となっています。この結果から、「授業への興味が高い人ほど成績がいい」と言えるでしょうか。相関係数0.15というのは、かなり弱い相関だと言えますので、「授業への興味が高い人ほど成績がいい」と明確に言い切ることは難しいと思います。では、この場合の結果はどのように報告したらいいのでしょうか。次のような記述でしたら誤解は生じないと思います。
授業への興味と成績の間には、正の相関があるが、その関連性は弱いと言える。
検定結果とデータ数の関係
このように相関係数が低くても、無相関検定では有意(相関はゼロではない)と判断されることがあります。これは、データ数が多いことに起因する可能性があります。相関の検定だけではなく、他の検定でも同様で、データ数が多いと検定仮説が棄却されやすくなるという特徴を統計的検定では一般に持っています。カイ二乗検定で、データ数が1,000の単位の研究を見ることがありますが、この場合は検定仮説を棄却しやすくなります。つまり、本当は検定仮説が正しいのに、誤って棄却されてしまう可能性がありますので、注意が必要です。
そこで、近年報告が求められるようになってきているのが効果量です。効果量は、例えば「平均値の差の検定」の状況では、「2つの母集団の平均値の差を母集団間に共通の標準偏差で割って標準化した値」で定義されます。その効果量は、「観測された2つの標本集団の平均値の差と各標本集団の分散および自由度(各標本集団の標本数の合計-2)」から推定します。数式で見るとt値が標本数に影響されるのに対して効果量は標本数に影響されないことがわかりますが、この連載の水準を超えますので数式は省略します。これはt検定に関係する効果量ですが、その他の検定法でも計算することができます。詳しくは、参考文献(例えば、西村・井上(2016))を見て下さい。ただ、気を付けないといけないのは、効果量は標本数の影響を受けませんが、計算された値は母集団での効果量ではなく、標本として観測されたデータから計算された効果量の推定値なので、標本変動の影響を受けることに変わりがない、ということです。また、効果量の大きさの評価にはどうしても主観的な判断が残ります。
このように効用と限界とを心得て使うべきです。特に統計法の初心者はやみくもに新しい指標や方法に飛びつくのではなく、そこで用いられている論理をしっかり理解することが大切です。「生兵法は大怪我の元」という格言を常に思い起こしながら、謙虚な姿勢で分析を進めましょう。
まとめ
最後に、今回の内容をまとめてみたいと思います。
カイ二乗検定
- 結果を報告する時には、クロス表を報告するのが一般的です。クロス表を提示すれば、どのように計算したのかが一目瞭然にわかります。
- クロス表には、観測度数と期待度数を記載することが望まれます。
- 有意確率が有意水準以下だった場合の結果は、「偏りがある」「関連がある」などと表現します。「有意差があった」とは言いません。
相関係数の検定(無相関検定)
- 2変量の一致度を見る場合は、相関ではなく、κ係数(カッパ係数)の方が適切です。
- 無相関検定は、「2変量の相関係数が母集団でゼロである」という検定仮説を検定するものなので、相関の「度合い」を見る場合は値を参照しなくてはいけません。
- 無相関検定をはじめとした検定の結果というのは、データ数の影響を受けるということを覚えておく必要があります。
参考文献
西村純一・井上俊哉(2016)『これから心理学を学ぶ人のための研究法と統計法』ナカニシヤ出版
野口裕之・大隅敦子(2014)『テスティングの基礎理論』研究社









