以前、『日本語教育』『社会言語科学』『世界の日本語教育』などの日本語教育関連の雑誌を対象に、どのような統計手法が多く使用されているか調べたことがあります。もっとも多く使用されていたのがt検定でした。t検定とは、2つの母集団の平均値の間に有意な差があるかどうかを調べるものです。今回は、このt検定について日頃感じることをまとめてみました。
統計的推測は全数データでは行わない
t検定のような統計的推測という統計手法は、母集団から抽出したサンプルデータに基づいて、母集団に関して差があるか否かを計算するものです。ですから、データが母集団の全データを扱うときには、この統計的推測の手法は使用しません。しかし、全データを扱っているにもかかわらず統計的推測法を用いた結果を掲載している論文を見ることがあります。そこで、先ずは、どういう場合に統計的推測を行うか、島田・野口(2017:vi)を以下に引用します。
緑色のりんごと赤いりんご、それぞれ1箱ずつあるとします。それぞれの箱には20個のりんごが入っています。緑色のりんごと赤いりんごは大きさに差がないと聞いていたのですが、緑色のりんごの箱と赤いりんごの箱から1個ずつりんごを取り出したら赤いりんごのほうが大きかったらどう思いますか。20個のうちの1個を比べただけですから「偶然かな」と思うのではないでしょうか。つまり、「本当は差がないけれど、たまたま選んだ赤いりんごが大きかったのだろう」と考えると思います。次に、両方の箱から5個ずつ取ったら、すべて赤いほうが大きかった場合はどうでしょう。「大きさに差がない」という前提が間違っていたのではないかと考えるのではないでしょうか。統計分析では、このように、得られた一部のサンプルデータ(この場合、たまたま箱から取り出したりんご)をもとに計算を行い、母集団(この場合、箱に入っている緑色のりんご20個と赤いりんご20個)において「差がない」という前提(統計分析で「仮説」と言います)が正しいかどうかを推定します。
このように、全データの情報が得られていない場合、統計手法を用いて、サンプルデータから全データについて推測できるのです。ですから、もし対象としているデータが母集団の全データであったら統計的推測は行いません。
20年ほど前、島田と野口は日本語教育学会の試験分析委員会の委員で、日本語能力試験の実施結果に関する分析を行っていました。そのころ日本語能力試験がスタートして10年の節目を迎え、過去10年の問題の分析を行うことになりました。島田は聴解類を担当し、談話や選択枝の特徴が結果に影響を及ぼしているかを分析しました。談話形式がモノローグかダイアローグかによって正答率の平均値に差があるかを調べるために、t検定を用いようとしたところ、「全データを分析しているのだからt検定をする必要がないし、してはいけない」と野口から指摘されました。確かに、母集団は日本語能力試験の聴解類の問題で、実際に扱っているデータは過去問題すべてでしたから、「母集団に関する推定」をする必要はなかったのです。そのころ、島田は、正しく「母集団の推定」の意味を理解していませんでした。野口の指摘がなかったら、危うく誤った分析を世に公表しているところでした。
母集団の全データが分析対象となっている場合は、推測統計の手法を用いずに、統計的記述の方法で分析します。統計的記述の方法というのは、この場合は、平均値、標準偏差、相関係数などを示すということになります。上記のt検定のほか、たとえば、Aという教科書とBという教科書で一人称の使われ方に違いがあるかカイ二乗検定を行うという場合、Aという教科書とBという教科書の全ての文を対象としているのでしたら、推測統計の手法(この場合、カイ二乗検定)を用いず、統計的記述の方法を用います。なお、統計的推測の方法が統計的記述の方法より優れているとかレベルが高いなどということはありません。統計的な分析で何を見たいのか目的に応じて決まるのです。
ところで、上記に「選択枝」と書きました。通常は「選択肢」と表記された文章を見ることが多いと思いますが、日本語能力試験をはじめ複数の試験では「選択枝」と表記されます。日本テスト学会が2007年に出版した『テスト・スタンダード—日本のテストの将来に向けて』で「選択枝」が採用されているため、テストに関する専門用語としては「選択枝」を用いるということなのだと思います。同書によると、「肢」という身体用語を避けたいということ、英語で設問部分をstem(幹)、選択肢をbranch(枝)ということから、「選択枝」を採用する理由が記載されています(p.18)。私どももこれにしたがって「選択枝」を用いています。
t検定を繰り返してはいけません
t検定は、冒頭に述べたとおり、2変量の間の平均値の差を検討する統計手法です。例えば、文法テストについて、中国語母語話者と韓国語母語話者とタイ語母語話者の平均値の間に差があるか否かを見たい場合、「中国語母語話者」と「韓国語母語話者」の間で検定、「韓国語母語話者」と「タイ語母語話者」の間で検定、「タイ語母語話者」と「中国語母語話者」の間で検定、というように、繰り返してt検定を行うことはできません。この例のように3つの母集団の間を検討したい場合は、分散分析法を利用します。このことは、t検定を解説する書籍には必ず書いてあることですが、t検定を3つの母集団間で繰り返し実施するという誤った使い方をしている論文を見かけることがあります。
では、なぜt検定を繰り返してはいけないのでしょう。少し丁寧に解説していきます。
① まず、「中国語母語話者」と「韓国語母語話者」という2つの母集団の場合を考えましょう。この場合の検定仮説は次のようになります。
仮説:「中国語母語話者」と「韓国語母語話者」の母平均の間には差がない。
有意水準を5%に設定した場合、有意確率5%以下だとこの仮説は棄却されます(「両者の母平均の間には差がある」という結果になります)。逆に、棄却されない(仮説を採択する)確率は95%になります。
② では、3つの母集団の場合はどうなるでしょう。
検定仮説はつぎのようになります。
仮説:「中国語母語話者」と「韓国語母語話者」の母平均の間には差がない。
かつ
「韓国語母語話者」と「タイ語母語話者」の母平均の間には差がない。
かつ
「タイ語母語話者」と「中国語母語話者」の母平均の間には差がない。
つまり、3つの母集団の場合の検定仮説は、すべての組み合わせで「差がない」ということです。この仮説を棄却するには、3つの組み合わせのうち少なくとも1つの組み合わせで「差がある」と判断されればいいのです。ここまでで、3つの母集団の方が「差がある」と判断されやすいということがわかると思います。
③ 最後に、3つの母集団の場合が2つの母集団の場合に比べて、具体的にどのぐらい「差がある」と判断されやすいのか考えてみましょう。5%水準の場合、仮説が棄却されない確率は、「中国語母語話者」と「韓国語母語話者」という2つの母集団については上記のとおり0.95(95%)です。
3つの母集団の場合は、仮説が棄却されない確率は、「中国語母語話者」と「韓国語母語話者」の間について0.95(95%)、「韓国語母語話者」と「タイ語母語話者」の間についても0.95(95%)、「タイ語母語話者」と「中国語母語話者」の間についても0.95(95%)です。これらすべてにおいて棄却されない確率は、「0.95×0.95×0.95」、つまり0.857ということになります。そして、棄却される確率は、「1-0.857」で、0.143となります。最初は有意水準0.05(5%)で考えていたのに、3つのうち少なくとも1つの組み合わせで棄却される確率は0.143(14.3%)になってしまうのです。ずいぶん棄却されやすくなるということです。ですから、3つの母集団のときは、t検定ではなく、分散分析法を使用する必要があります。あるいは、水準を厳しくして、t検定を繰り返し実施する例を見ることもあります。
平均値だけではなく標準偏差も報告しましょう
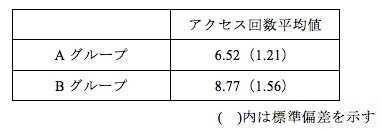
t検定は、平均値の差の検定ですが、t値は標準偏差(分散)の大きさも影響します。そのため、必ず標準偏差も報告しなければいけないのですが、残念ながら標準偏差が報告されていない論文が非常に多いです。表に書き込むときは、下の表1のように、平均値を示し、標準偏差は( )に書くことが多いです。しかし、そのことを知らない読者もいますから、必ず、表1のように「( )内は標準偏差を示す」ということを明記する必要があります。
表1 E-learningアクセス回数平均値
また、グラフで平均値を示し、標準偏差を示していない場合もありますが、やはり、必ず標準偏差を示さなければいけません。なかには、グラフに平均値がはっきり明記されていない図1のような例もあります。図1は、聴解テストの問題の内容別に、英語母語話者と中国語母語話者の得点の平均値を示したものです。連載の初回に書きましたが、このような図は平均値を示すにはふさわしくありません(理由は第1回「そのグラフ、大丈夫ですか」をご覧ください)。しかし、平均値を示すのにこのようなグラフを用いる論文が非常に多いのも事実です。図1の場合は、おおよその平均値はわかりますが、正確な平均値、そして標準偏差の情報が書かれていません。著者はグラフで示しているのでわかりやすいと考えているのかもしれませんが、t検定に必要な平均値と標準偏差は明記されなくてはいけません。
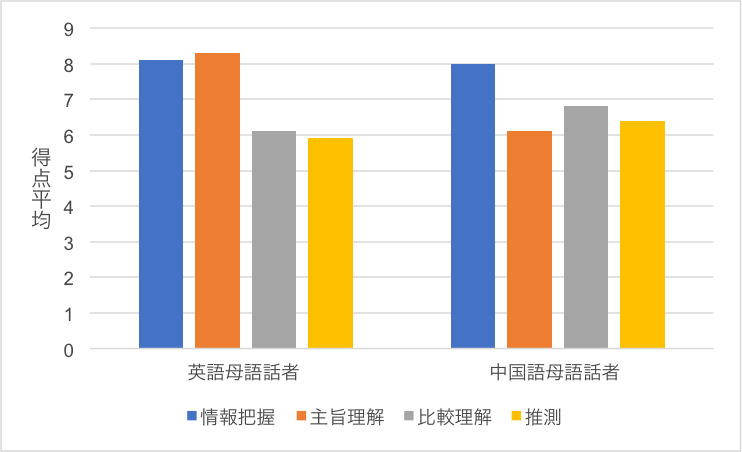
図1 聴解テストの結果
必要な情報、書いていますか
統計手法が用いられている論文を読むと、大事な情報が書かれていない例をたびたび見ます。
例えば、図1のグラフを示し、結果(t検定の結果)については次のような記述が書かれていたとしたらどうでしょう。
「情報把握」「比較理解」「推測」は両者の間で有意差は見られなかったが、「主旨理解」に関しては英語母語話者の方が中国語母語話者より有意に平均値が高かった(t(52)=3.50, p<.01)。
この記述では、有意差が観察された「主旨理解」についてはt値などが報告されていますが、差がなかった他の問題については「有意差は見られなかった」ですまされています。「有意差が見られなかった」のも結果ですから、これらも含めて、すべてのt検定の結果を示さなくてはいけません。
ところで、t検定には、等分散が仮定されるという条件があります。次の例を見てください。
2つのグループの得点を比較したところ、等分散ではないことがわかったため、ウェルチのt検定を行った。
この例では、等分散であるかを確認していることがわかります。しかし、その結果を導いた方法や数値が提示されていません。「等分散ではない」ということの根拠を示す必要があります。
知りたいことが本当にわかるデータを使っているかよく考えましょう
対応のないt検定は、平均値、標準偏差がわかっていれば計算できます。そのため、自分が収集したデータと先行研究のデータ(平均値と標準偏差)を使い、母平均に差があるかt検定を行うことを考える人がいます。例えば、5年前の先行研究で、英語母語話者を対象に行った日本語に関する自己評価得点の結果(人数と平均値と標準偏差)がわかっています。自分はベトナム語母語話者を対象に同様の調査を行ったので、英語母語話者グループとベトナム語母語話者グループの母平均の間に差があるか検討するというような例です。この場合、有意差があったとしても、母語の違いだけではなく、5年という時期の違い、学習環境、学習方法、年齢、そして何よりも2つの調査の目的や実施方法などの諸条件や拠って立つ理論的基盤の違いなどが影響している可能性を否定できません。つまり、仮説を検証することは難しいと言えます。これは極端な例ですが、先行研究ではなく自分で収集したデータを使用する場合でも、知りたい要因(例えば母語の違い、日本語能力レベルの違いなど)以外に、結果に影響を及ぼす要素がないかよく考える必要があります。
まとめ
今回は、t検定の結果を報告する論文を読んでいて気づいたことを書きました。まとめると次のようになります。
- t検定のような統計的推測という統計手法は、母集団から抽出したサンプルデータに基づいて、母集団に関して差があるか否かを判断するものですから、対象とする母集団全体が分析データとなる場合には、統計的推測ではなく、統計的記述の方法を取ります。
- t検定は、2つの母集団間で平均値が異なるか否かを検討する方法であるということを忘れてはいけません。ですから、3つの母集団間で平均値が等しいという仮説を検定するのに、同じデータに対して組み合わせを変えて繰り返し計算してはいけません。3つの母集団間の平均値の差を検討する場合、2つの母集団間で検討する場合よりも、検定仮説が棄却しやすくなる、つまり本当は差がないのに「差があった」と結論付けてしまう可能性があるからです。
- t検定の結果を報告するときは、平均値だけではなく、標準偏差も報告します。
- 単に「有意な差は見られなかった」だけではなく、その根拠となる数値も報告します。また、「等分散ではない」場合も、どのように計算したか根拠を示す必要があります。
- 知りたい要因(例えば母語の違い、日本語能力レベルの違いなど)以外に、結果に影響を及ぼす要素がある場合はt検定を行っても意味がありません。
引用文献
島田めぐみ・野口裕之(2017)『日本語教育のためのはじめての統計分析』ひつじ書房
日本テスト学会(2007)『テスト・スタンダード—日本のテストの将来に向けて』金子書房









