修士論文、雑誌に掲載された論文を読むと、結果の記述のしかたに疑問を感じることが時折あります。今回は、そのような中でも、統計に関する基本的な理解が不足していることに起因すると思われる例を取り上げたいと思います。

 

有意差が出ない結果も結果です

大学院生を対象にした統計分析の授業で、「有意差が出なくても、想定していたのと違う結果でも、それが結果ですから、それを受け入れましょう。」と口をすっぱくして言います。そのときは、学生もうんうんとうなずきます。ところが、実際に自分たちでデータを収集して分析をする演習の段になると、この言葉はすっかり忘れられてしまうようで、分析した結果、有意差が得られなかった学生は肩を落としてがっかりします。また、修士論文を執筆している学生からは、「t検定をしましたが、有意差が出ません（涙）」、「有意差が出なかったので、失敗です」、ひどいときには「t検定では有意差が出ないので、カイ二乗検定をしてみたいです」などと言われることがあります。そして、納得のいく結果（有意差が出る結果）を求めて、いろいろな方法を試そうとします。その度に、「差がない、ということも結果ですよ」「差があると思ったのに差が出なかったんでしょう？　それは発見ですね」などと言います。「有意差が出ないと研究が失敗だ」「何としても有意差を得たい」という考え（場合によってはそういうこともあるかもしれませんが）は、極端に走ると、都合の悪いデータを削除して有意差を導き出すという「改ざん」につながる可能性を秘めています。差があると考えて研究を進めていて、差が出なかったとしても、それは立派な結果ですから、受け入れなければなりません。

しかし、どうしても検定結果が受け入れられないのか、発表された論文の中に、次のような記述を見ることがあります。

「t検定の結果、日本語母語話者とモンゴル語母語話者の平均値の間に、有意差は認められなかったが、両者の差は2.5ポイントと大きな差があった。」

「検定の結果、有意差は認められなかったんだけど、差は大きい」と言っているわけですから、矛盾したことを言っていることになります。t検定の結果有意差が認められなかったということは、「2つの母集団の間で、なんらかのデータに関し、平均値に差はない」という仮説を棄却できなかったわけですから、たとえ差があるように思える数値であっても、統計的には「差がある」とは言えないのです。確かにデータを得た２つの標本集団の平均値には差がありますが、t検定の結果からは２つの母集団の平均値に差があるとは言えないのです。統計分析をすると決めたのなら、どのような結果でもそれを受け入れるべきです。もちろん、データのサイズやある種の偏りなどが結果に影響を与えるので、もしかしたら、統計分析を実施すること自体が適切ではないという場合もあるでしょう。「どうしても統計的に分析しなければいけない」「有意差が認められないとだめだ」と思っている大学院生が多いようですが、まずは、自分のデータをどのように分析するか、統計分析が必要か、ということをよく考え、統計分析を行うのであればその結果を受け入れる必要があります。

 

「有意傾向」に注意

統計分析の結果を表す表の下に次のように書かれているのを見たことがある人は多いでしょう。

^† p< .10   * p< .05   ** p< .01

表中に*が付されているものは「p値（有意確率）が0.05（5%）以下である」ということ、 **は「有意確率が0.01（1%）以下である」ということを意味しています。つまり、どちらも「有意である」ということになります。では、^†（ダガー）はどういうことでしょう。これは、「有意確率が 0.05（5%）を超え 0.10（10%）以下である」ということを示していて、この場合の結果を「有意傾向」と言う研究者がいます。この「有意傾向」について少し考えてみます。

まず、有意水準、すなわち有意確率がどの程度であれば有意とみなすかは、分野によって、また研究者によって異なります。理論的には「研究者が設定する」ということにはなっていますが、勝手に個々の研究者が設定しては、相互の結果を比較したりできませんから、やはり分野の一般的なルールに従うのが望ましいでしょう。言語教育の分野では、有意水準は、通常5%を採用します。どういうことかt検定の場合で説明します。まず、なんらかの数値（テストやアンケートの点など）について「２つの母集団の平均値の間には差がない」と仮定します。これを検定仮説（帰無仮説）と言います。その2つの母集団からランダムにサンプルデータを得てt値を計算したところ、その結果の有意確率が0.05（5%）以下だったとします。0.05（5%）以下ということは、100回サンプルを取って計算しても5回以下しか出現しないような「滅多に起きない値」が得られたということです。このような稀にしか得られない値だったら、「そもそもの検定仮説が間違っていて、2つの母集団の平均値には差があったんだ」と判断し、検定仮説を棄却します。もし、「両者には差があるに違いない」（検定仮説が棄却できる）と思っていて、t検定を行った結果、有意確率が 0.055（5.5%）だったらどう思いますか。5%を超えていますから検定仮説を採用し「両者の平均値の間には差がない」という結果になります。差があることを期待していると、「たった0.005超えているだけなのに惜しいなあ」と思うかもしれません。先述のとおり、このような、有意確率が0.05（5%）を超え 0.10（10%）以下の時に「有意傾向」と報告する研究者がいます。これ自体は間違いではありませんが、あくまでも有意水準（5%）より大きいわけで、「有意差がある」とは言えないのです。しかし、まるで有意差があるように書かれている記述を見ることがあります。たとえば、次のような表を示し、以下のような記述がなされていることがあります。

表1　t検定の結果（例1）

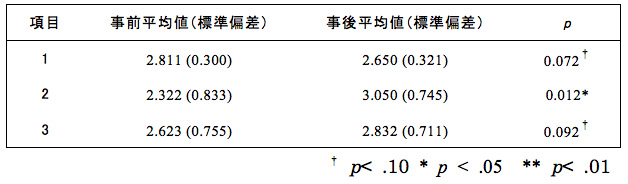
記述例：t検定の結果、3項目すべてにおいて統計上有意な差が観察された。

この例は、事前アンケートの結果と事後アンケートの結果を比較したものです。表を見ると、有意確率（表ではpで示しています）が0.05（5%）未満、つまり、事前と事後の平均値の間に有意差が認められるのは項目2のみであり、それを示すアスタリスク（*）が付されています。しかし、記述例を見ると、項目1も項目3も「有意な差が観察された」と述べています。これはどういうことかと言うと、項目1と項目3の結果（有意確率）は、0.05（5%）を超え0.10（10%）以下なので「有意傾向」ということになり、それを「有意差あり」と記述しているのです。繰り返しますが、「有意傾向」は「有意差がある」のではありません。しかし、このように、あたかも差があったかのように報告する論文があります。このような記述をするということは有意水準に0.10（10%）を採用したことになってしまいます。

もしかしたら、先の例で、筆者が「差がない」という結果を期待していたら、「項目2のみ差があった」と言うのかもしれません。そういう意味で、この「有意傾向」には注意が必要です。「有意傾向」と報告することは間違いではありませんが、有意水準を決めて計算する以上、検定仮説を棄却するか採択するか二者択一とするべきだと多くの研究者は考えます。大学院生や統計の初心者は、もしかしたら「有意傾向」と報告している先行研究を見て、「有意傾向も報告しなければいけない」と思っているのかもしれません。しかし、決してそうではないことを理解してほしいと思います。

 

「有意確率」の意味をもう一度考えましょう

皆さんは、次のような記述を読んでどう思われるでしょう。

「韓国語母語話者と中国語母語話者の読解のテスト結果は、t検定の結果、5％水準で有意差が認められたが、文法のテスト結果は、1％水準で有意差が認められた。このことから、文法テストの方が平均値の差が大きいと言える。」

繰り返しになりますが、この5%、1%というのは、有意水準、つまり、「差がない」という検定仮説（帰無仮説）のもとで、実際に観測された結果が「稀にしか出現しないと判断する」と当該研究者が決めた確率です。この確率が小さいと、滅多に起きない状況と判断され、検定仮説が間違っていたと判断されます。このように、有意水準は、検定仮説を棄却するのか採択するのかを決定するための基準であり、平均値の差の大きさを示したものではないのです。ところが、この確率が小さければ小さいほど「いい」「差が大きい」と考える人がいるようです。この例のように、出現確率の大きさを比較するのは誤りです。

また、以前、有意確率を小数点以下7位まで記載してある論文を見たことがあります。どうなるかというと、「0.0000013」ということです。統計分析で大事なのは「検定仮説を採択するか棄却するか」なので、有意確率をここまで細かく報告する必要はまったくありません。0.001と0.0001を区別する必要はないのです。「p < .01」（1%水準）で十分ということです（「p < .001」（0.1%水準）を記載する場合もあります）。

今は統計ソフトで計算すると、一瞬で、t値もp値も正確に算出されます。しかし、コンピュータが今ほど普及していない頃は、自分でt値を計算し、t分布表を見て、その値と自由度の組み合わせで有意確率（p値）を見つけました。表2は、海保（1985）のt分布表をもとに作表したものです。たとえば、t検定の結果、自由度が26で、t値が2.200、と計算されたとします。有意確率を確認するために、t分布表（表2）を見ます。一番左の列が自由度を表していますので、「26」の行を見ます。「26」の右に書いてある数字が５つの有意水準αに対応するt値です。計算されたt値が2.200だとしましたから、「2.056」と「2.479」の間に入ることがわかります。「2.056」と「2.479」それぞれの列の上部を見ると、「.050」と「.020」と書いてあります。これがそれぞれのt値に対応する有意確率（有意水準）で、「.050」と「.020」の間ですから、有意確率は「p<.05」だということがわかります。表2には有意確率（有意水準）は、.200、.100、.050、.020、.010　の5つしかありません。つまり、.010より小さいかどうかは問題になるけれど、それより小さい場合、その大きさは考慮しない、ということを示しています。

表2　t分布表

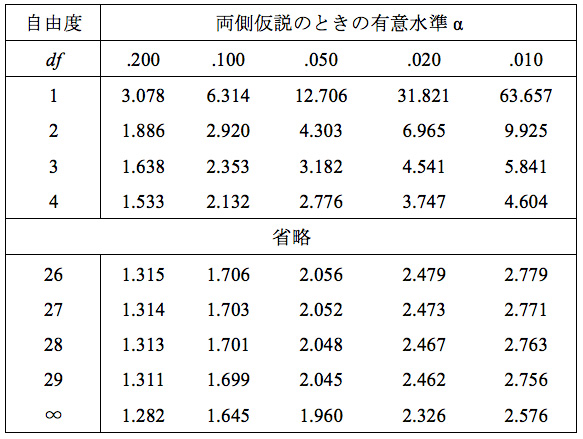
海保（1985）を参考に作表

以前は、p値を細かく報告できなかったわけですが、今は簡単に計算できるので、そのとおりに正確に記載しようと、先の例では「0」をたくさん書いたのだと思います。しかし、出現確率の意味を正しく理解すれば、このようなことは起きないと思います。

 

確率の表記は .05 ? それとも 0.05 ?

ところで、読者の中には「なぜ有意確率や有意水準のような確率を「0.05」ではなく「.05」と書くのか」、あるいは「どちらの記述もあるけれど違いはないのか」などと思われる方もいることでしょう。このことも統計の本などにはあまり書いてありません。有意水準を表す場合は、「0.05」でも「.05」でもいいのですが、通例的に後者を使うことが多いです。なぜ「0」を省略できるかというと、確率ですから、必ず 0から1の間の数値になり、小数点以下に0以外の数値が生じた場合、一の位は「0」に決まっているからです。確率に「1.05」や「5.05」という値になる可能性はないということです。ですから、このように一の位が0だとわかっている場合は、0を省略できるのです。そのほか、相関を表すときも同様です。相関係数は、-1から1の間の値のため、小数点以下に0以外の数値があったら、一の位は「0」以外にありえません。

次の表3は、初級学習者と中級学習者の、自己評価の平均値と標準偏差、t値を表しています。どこがおかしいでしょうか。

表3　t検定の結果（例2）

初級学習者の標準偏差を見てください。「.98」となっていますので、おそらく「0.98」なのだと思いますが、標準偏差の場合は一の位が0とは限りませんので、0を省略することはできず、「0.98」と書くべきです。もう1箇所、t値を見てください。「.04」と書かれていますので、おそらく「0.04」なのだと思います。t値も一の位が0とは限りませんので、省略できません。

確率や相関の「0」を省略できる理由を理解していれば、標準偏差やt値やF値を表すときに一の位を省略できないことは明白です。ところが、上の表のように省略している報告を時々見ます。おそらく、省略の理由を理解せず、出現確率や相関係数で一の位の「0」が省略されているのを見て、自動的にほかの「0」も省略してしまったのではないでしょうか。あるいは、先行研究を見て、同じように書いてしまったのかもしれません。

 

まとめ

今回は、統計の基本がよく理解できていないために起こる誤りを見てみました。まとめてみると、次のようになります。

1. 統計処理を行ったのであれば、有意水準をもとに有意差があったかなかったかを報告しましょう。検定仮説（帰無仮説）を棄却できなかったのに「差は大きい」と報告したり、有意傾向であるのに「差があった」と報告するのは誤りです。

2. 有意確率の違いは、差の大きさの違いではないので、「p<.01はp<.05よりも差が大きい」とは言えませんし、小数点以下2位あるいは3位までの報告で十分です。

3. 「.01」のように一の位を省略できるのは、確率や相関など、最大の値が絶対値で1の場合のみです。

引用文献

海保博之（1985）『心理・教育データの解析法10講 基礎編』福村出版