あちらこちらで発表された修士論文を見ると、最近は授業で統計手法について学ぶ機会もあるようで、多くの学生が統計手法を用いています。しかし、基本的な誤り、特に報告の仕方に誤りが少なからず見られます。本当に基本的なこと、基本中の基本は、当たり前すぎて、統計入門の本には書いていないのかもしれません。この連載では、当たり前すぎてどこにも書いていないようなことを考えていきたいと思います。
グラフの「大量生産」
初回は、グラフを取り上げたいと思います。なぜかというと、多くの学生がグラフを使うと効果的だと思っているようで、大量生産されているように思うからです。また、世に出ている論文を見ても、疑問に思うことがあります。
グラフの大量生産については、言語テストの専門家J. D. Brown も著書Using Surveys in Language Programsの中で、若手研究者はグラフをレポートの中で多用しすぎており、それらは効果的とは言い難いと、グラフの使いすぎを警告しています(Brown 2001: 118)。「グラフを使わなくてもいい」と言う例は後半取り上げますが、その前にグラフに関する基本的な誤りを見ていきましょう。
図には必要な情報を盛り込む
まず、基本中の基本ですが、図は、本文を読まずとも、それだけで何が示されているか理解できる情報が盛り込まれている必要があります。ところが、何を示しているのかわからない、という場合は少なくありません。グラフを見て、縦軸に単位が書かれていないので何を表しているのかわからない、字が小さすぎて読めない、カラーで作成したグラフを白黒コピーしたためどの棒が何を表しているか識別できない、などと思ったことは少なからず経験があるのではないでしょうか。グラフはExcelなどで簡単に描けるので、そのままコピー・ペーストしてしまうことが大きな問題ではないでしょうか。一手間入れて、情報を追加するなどの作業をしてほしいです。
例えば、次の図1は、授業受講者25名に行ったアンケート調査の結果です。質問に対する回答は5段階でなされているということは本文でわかったとしても、グラフが表す数値(質問1の4.2、質問2の4.8、質問3の3.8)は何を指すのでしょう。勘がいい人はすぐわかると思いますが、平均値を表しています。しかし、どこにも平均値とは書かれていません。必要な情報は図の中やタイトルに盛り込むべきです。
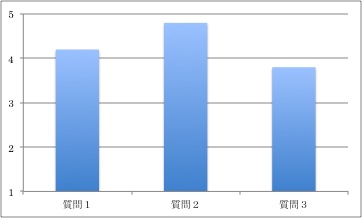
図1 アンケートへの回答
次の図2のタイトルは「レベル別あいづちの使用頻度」です。ということは、単位は何回使用したかという回数になるはずですが、図を見ると%となっています。図のタイトルは「レベル別あいづちの使用割合」や「レベル別あいづちの使用率」などとするべきでしょう。このように、図のタイトルは「頻度」、グラフの単位は「%」となっているグラフも少なくありません。
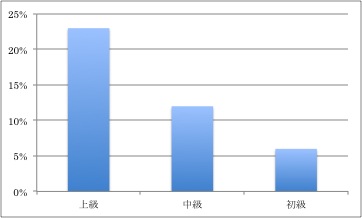
図2 レベル別あいづちの使用頻度
人気の高い棒グラフですが
日本語教育関連の雑誌に掲載されている論文をざっと見たところ、もっとも多いのが各種棒グラフです。棒グラフはどのようなものを表すのに適しているでしょうか。総務省統計局のウェブページに「なるほど統計学園」なるものがあり、グラフの種類が解説されています。このページによると、「棒グラフは縦軸にデータ量をとり、棒の高さでデータの大小を表したグラフ」とあります。言語学や言語教育の場合ですと、ある言語形式の出現頻度、学習者数などが考えられるでしょう。
次の図3は、野畑・ガムチャンタコーン(2006)の「タイにおける中等学校日本語教員養成講座の概要と追跡調査報告:タイ後期中等教育における日本語クラスの現状」から引用したもので、「日本語を開講している中等教育機関数の変化」というタイトルの図です。このグラフは積み上げ棒グラフというもので、複数のデータを積み上げて示すものです。このグラフでは、学校数を明示する図であり、典型的な例と言えます。このように、棒グラフはなんらかの数(人数、学校数、使用回数など)を示します。
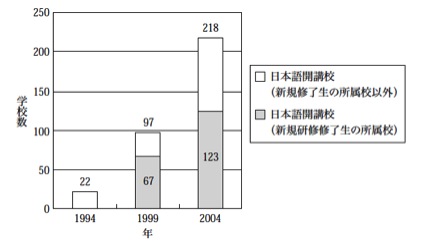
図3 棒グラフの例
(野畑・ガムチャンタコーン(2006: 178)より引用、
引用元タイトル:日本語を開講している中等教育機関数の変化)
表1は、以前私が書いた論文から引用したものです(島田・侯 2009:37)。この論文ではグラフは描いていません。必要な情報は全てこの表の中に表されているため、これで十分と考えるからです。しかし、このような表があるにもかかわらず、図4のような棒グラフも合わせて示している論文等がとても多いです。特に大学院生が書く修士論文には多発しています。この論文では、聴解テストのフォーム1とフォーム2の得点には大きな差がないことを示しているのですが、表だけではわかりにくいでしょうか。もしかしたら図の方がわかりやすいという方もいるかもしれませんが、図4では、標準偏差、つまり、どの程度得点が散らばっているかという情報はわからず、中途半端な情報が提示された感じがします。特に、t検定や分散分析などで平均値の差の検定を行っている場合は、散らばりの情報が必要ですので、このような図では不完全と言えるでしょう。
表1 テストの記述統計量

(島田・侯(2009:37)より引用)
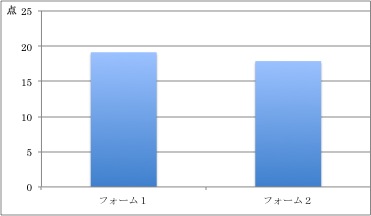
図4 テストの平均値
教育心理やテスト理論の分野では、平均値を棒グラフで表すことはあまり多くなく、まずは表で示すのが基本だと考えていいでしょう。しかし、学会発表などで視覚的に見せたほうがわかりやすい場合や、論文中でも図の方がわかりやすい場合もあるでしょう。そのような場合は、図5のように示すことできます。図5は、手前味噌ですが、島田・三枝・野口(2006)「日本語Can-do-statementsを利用した言語行動記述の試み:日本語能力試験受験者を対象として」の中で用いた図です。あるCan-do記述文について、レベルごとの平均値と標準偏差を示しています。グラフ内の小さい□は平均値、□の上下に伸びている縦線は±1標準偏差を示しています。また、本文がないのでわかりにくいですが、図の縦軸の「CD1」とは「Can-do記述文1番」という意味です。
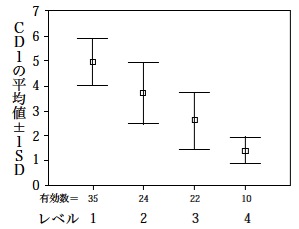
図5 平均値と標準偏差を示すグラフ
(島田・三枝・野口(2006:82)より引用、
引用元タイトル:項目1のレベル別平均値・標準偏差)
また、棒グラフに散らばりを示すためにエラーバーを加えるという方法もあります。日本語教育の論文でエラーバーを示したグラフを目にすることは多くありませんが、李(2006)の「在日台湾人子どもの読解力の測定:中国語母語話者と日本語母語話者の読解力を比較分析する」という論文の中に見つけました。図6を見ると、棒の上に飛び出たTの文字のようなものがあります。これをエラーバーと言い、データの散らばりを示すもので、データの標準偏差や平均値の標本変動の大きさを表わす標準誤差などが用いられます。この図の場合は、明記されていませんでしたが、標準偏差が用いられていると考えられます。この図を見ると、「接続」は、「在日群」(在日台湾人)の結果は散らばりが大きいですが、「統制群」(日本語母語話者)の結果は散らばりがない(つまり、全員同じ得点だった)ということがわかります。
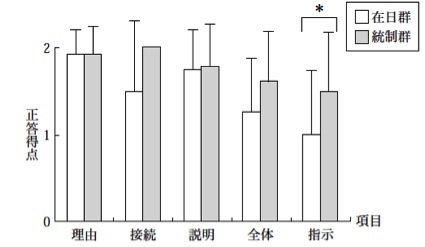
図6 エラーバーつき棒グラフの例1
(李(2006: 29)より引用、
引用元タイトル:中国語読解力の平均得点)
図6は、エラーバーがT字状でしたが、次の図7のようにカタカナのエ状の場合もあります。平均値(棒の一番上)から上下にエ状の棒が出ていますが、上下の長さは同じなので、上記の図6のように、下部を省略してT字状にすることも多いです。
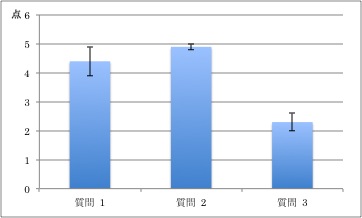
図7 エラーバーつき棒グラフの例2
以上見てきたように、平均値を示す方法として、単純な棒グラフは推奨できる方法とは言えませんが、日本語教育分野の論文では意外に多く見られます。問題は、大学院生など若手研究者がそういった例を模倣してしまうことです。グラフ一つとっても、きちんと調べることが大切ですね。
統計分析にカイ二乗検定という検定がありますが、カイ二乗検定では表2のようなクロス集計表を用います。表2は、森山卓郎(2009)『国語からはじめる外国語活動』の表を一部改編したものです。面白い内容なので、簡単に紹介したいと思います。小学生に次の文章を読んでもらい、Bさんがどこにいるか答えてもらうというものです。
AくんはBさんをさがしています。運動場の近くで、Dさんに「Bさん、どこか知っている?」とたずねると、Dさんはこういいました。「Bさんは運動場であそんでいるじゃない」
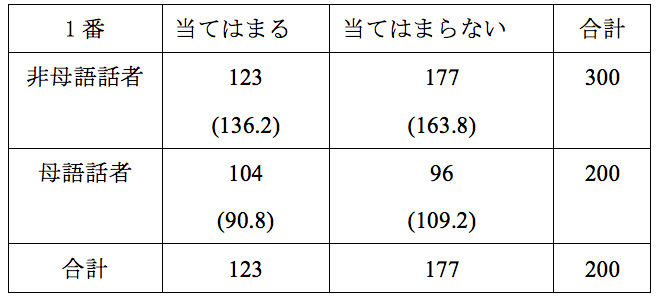
慌てて読むと間違えてしまいそうですが、正答は「運動場にいる」です。小学3年生と6年生の結果を示したものが表2です。学年の違いが結果に影響を与えているかを調べるためにカイ二乗検定を実施しています。カイ二乗検定では、観測値と期待値の2種類の数値が必要です。観測値は、3年生で正答したのは21人なので、この21が観測値となります。期待値は、表2では( )で示されていますが、全体の傾向(151人中73人が正答)から考えると、3年生で正答すると期待されるのは30.5人である、というように計算し、この30.5が期待値となります。カイ二乗検定の結果は表2のようなクロス集計表を示すのが通常です。しかし、日本語教育分野の論文には、棒グラフで表しているものがあります。
表2 クロス集計表の例1
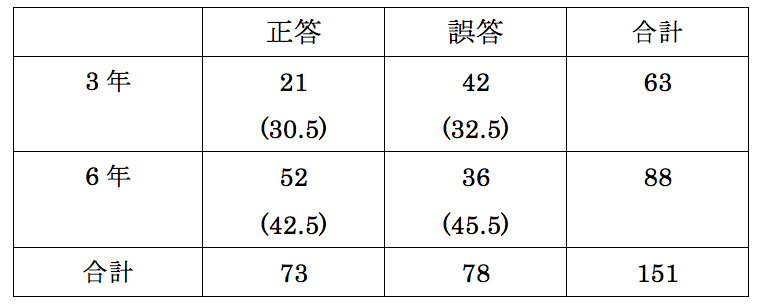
(森山(2009)の表を一部改編)
図8は、あるアンケートを日本語非母語話者と日本語母語話者に実施した結果を表しています。各項目の結果を非母語話者と母語話者にわけて図に表しています。確かに、どちらのグループも1番で「あてはまる」を選んだ人が多いことや4番は両グループの間に差があることなどが一目でわかります。しかし、この図では、どのようなカイ二乗検定を行ったのかが全くわかりません。おそらく、表3のクロス集計表のように、各質問項目について2×2のカイ二乗検定の結果を行ったのだろうと推測できます。各項目を選んだ人数は示されず、図8のように割合しか示されていませんので、観測値と期待値を知るには、回答者の人数から計算しなくてはいけません。図で示す方がわかりやすい、という意図があるのだと思いますが、かえってどのような分析をしたのかがわからず、逆効果と言え、避けるべきです。
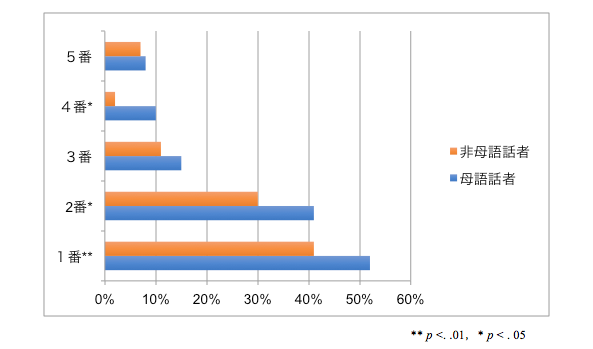
図8 カイ二乗検定の結果をグラフ化した例
表3 クロス集計表の例2
棒グラフとヒストグラムの違い
次の図9は宮本・倉元(2017)の「国立大学における個別学力試験の解答形式の分類」という論文中の「記述式問題の出題数の分布(前期日程)」というタイトルの図で、大学における記述式問題の出題数の分布を表したものです。160以上240未満の出題数の大学が21校ともっとも多いのがわかります。このようなグラフをヒストグラムと言います。棒グラフとの違いはなんでしょう。棒グラフは、棒と棒の間にスペースがありますが、ヒストグラムでは隣同士の棒がお互いに接しています。ヒストグラムは、各階級に含まれるデータ数を棒で表している点で棒グラフと同じです。しかし、階級が連続していると言う点で棒グラフとは違うのです。階級が連続しているから、棒と棒の間にスペースを入れません。言語教育分野では、テスト得点などで使用することが多いグラフです。逆に、階級が連続していない場合は、スペースを入れて棒グラフにしなくてはいけません。ところが、連続性のないカテゴリーなのにヒストグラムが使用されている例も見ます。
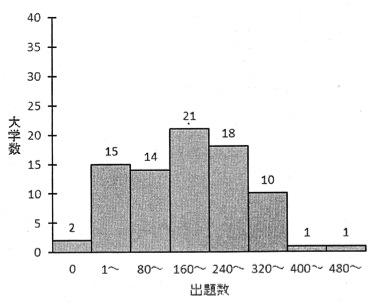
図9 ヒストグラムの例1
(宮本・倉元(2017:75)から引用、
引用元タイトル:記述式問題の出題数の分布(前期日程))
不要な棒グラフが多く使用されていることはすでに指摘したとおりですが、データの分布を見るためには、ヒストグラムで表すことは非常に有益です。次の表4は、島田・野口(2017)からのものですが、あるテスト得点の分布を表す度数分布表です。これをヒストグラムで表したものが図10です。いかがでしょうか。断然、図のほうが分布の様子がわかりやすいのではないでしょうか。このような図こそが効果的と言えるグラフだと思います。
表4 度数分布表例
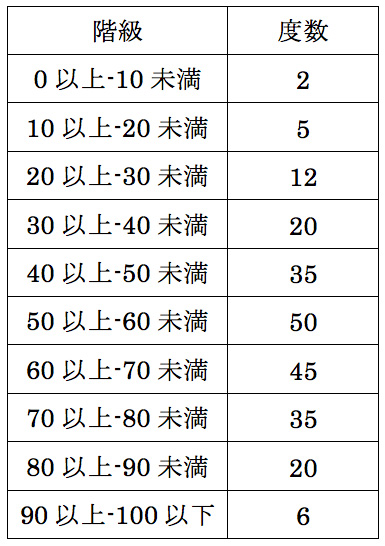
(島田・野口(2017:6)より引用)
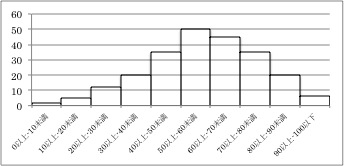
図10 ヒストグラムの例2
(島田・野口(2017:7)を元に作図)
散布図からわかることは多い
棒グラフは多用されすぎていると書きましたが、逆に図に示してほしいなと思うデータが相関係数です。相関関係を図に表したものが散布図です。相関係数を計算する論文は多く、相関係数と無相関検定の結果のみを示すものが多いです。
たとえば、クラスで読解テストと文法テストを行い、その関連性を見ようとして、相関係数を計算したところ、0.790でした。比較的高い値だとは思いますが、思っていたよりも低かったり、他の結果と比べると低い値だと思ったりするかもしれません。そこで散布図(図11)を確認すると、他の学生と異なる傾向を示す学生がいるのがわかります。この学生は読解テストは40点(平均点以上)なのに、文法テストは10点(最低点)です。このように、散布図を描くことにより、相関係数が(予想していた数値よりも)低い理由がわかる場合があります。ちなみに、この学生を除いて相関係数を再度計算すると0.926になりますが、この学生を計算から除外するかどうかは、計算の目的やこの学生が異質である理由などによるので、慎重に考える必要があります。
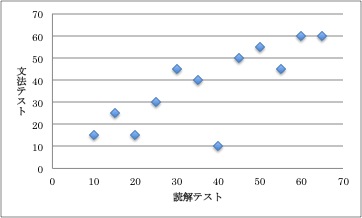
図11 散布図例1
また、次の例は、読書量(1ヶ月に読んだ本の冊数)と読解テストの結果の関連を調べたものです。相関係数は、0.630です。散布図を見ると、ある程度までは読書量が多いほど読解テストの得点は上がりますが、ある程度に達すると横ばいだということがわかります。このような傾向は、相関係数という数値にまとめてしまうとわかりません。
散布図を論文中に示すかどうかは、その内容によりますが、データ分析の過程ではぜひ散布図を描いて確認してもらいたいものです。
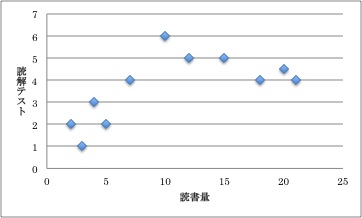
図12 散布図例2
まとめ
今回はグラフについて日々感じることをまとめてみました。今回のポイントをまとめると、次の3点になります。
1. 読み手がグラフだけを見て、グラフが何を表しているのか理解できるよう、必要な情報はすべて盛り込む。
2. 表のほうが情報を適切に表せる場合はグラフ化する必要はない(たとえばカイ二乗検定検定)。
3. グラフ化することにより得られる情報が多い場合は、グラフ化する(たとえば、ヒストグラムや散布図)。
次回は統計結果の記述のしかたについて考えたいと思います。
引用文献
Brown, J. D. (2001). Using Surveys in Language Programs. Cambridge University Press.
島田めぐみ・侯仁鋒(2009)「中国語母語話者を対象とした日本語聴解テストにおける選択肢提示形式の影響」『世界の日本語教育』19、国際交流基金、33-48
島田めぐみ・三枝令子・野口裕之(2006)「日本語Can-do-statementsを利用した言語行動記述の試み:日本語能力試験受験者を対象として」『世界の日本語教育』16、国際交流基金、75-88
島田めぐみ・野口裕之(2017)『日本語教育のためのはじめての統計分析』ひつじ書房
野畑理佳・ウィパー・ガムチャンタコーン(2006)「タイにおける中等学校日本語教員養成講座の概要と追跡調査報告:タイ後期中等教育における日本語クラスの現状」『世界の日本語教育』16、国際交流基金、169-187
宮本友弘・倉元直樹(2017)「国立大学における個別学力試験の解答形式の分類」『日本テスト学会誌』13-1, 70-84
森山卓郎(2009)『国語からはじめる外国語活動』慶應義塾大学出版会
李美靜(2006)「在日台湾人子どもの読解力の測定:中国語母語話者と日本語母語話者の読解力を比較分析する」『世界の日本語教育』16、国際交流基金、19-33
総務省統計局URL「なるほど統計学園」
http://www.stat.go.jp/naruhodo/c1graph.htm#section01(2018年2月2日閲覧)








